Geometría hiperbólica

 Semiplano de Poincaré (H) :

Hay un tipo de transformaciones del plano euclídeo que no dejan invariante la longitud de un segmento aunque sí transforma rectas en rectas, mantiene el paralelismo y también la medida de los ángulos; son las homotecias.

Ahora vamos a definir un modelo de geometría no euclidiana, es decir en la que no es válido el llamado 5º postulado de Euclides que afirma que por un punto exterior a una recta pasa una y sólo una recta paralela a ella. 

Se trata de la geometría hiperbólica, cuya métrica sí será invariante por homotecias.

El espacio de esta geometría se llama Semiplano de Poincaré y lo forman los puntos del plano euclídeo situados por encima del eje horizontal, es decir los que tiene su ordenada (la segunda coordenada) positiva.

Denotaremos este espacio con el símbolo Η. Observemos que Η no incluye al eje horizontal.

En esta geometría las "rectas" son:

1. Las rectas verticales del plano euclídeo, es decir las perpendiculares al eje horizontal -se entiende la parte que esas rectas tienen en H; y
2. Los semicírculos con centro en puntos del eje horizontal.

Estas "rectas" son suficientes para cumplir los dos primeros postulados de Euclides:

1. Por dos puntos cualesquiera pasa una única recta.
2. El segmento que determinan dos puntos cualesquiera puede prolongarse indefinidamente dentro de la recta que lo contiene.

En efecto, dados dos puntos cualesquiera A y B, existen dos posibles situaciones:

a) que A y B estén alineados en una recta vertical, en tal caso ya cumplen los dos postulados porque por ellos pasa una recta normal del plano euclídeo:

b) que no estén alineados en vertical, 

en ese caso existe un único círculo del plano euclídeo que pasa por A y  por B teniendo su centro en el eje horizontal (el centro del círculo es la intersección de la mediatriz del segmento AB con el eje horizontal). La mitad superior de ese círculo es una recta hiperbólica que pasa por ambos puntos:

Paralelismo en la geometría hiperbólica

En esta geometría por un punto exterior a una recta pasan infinitas rectas paralelas a ella, por ello incumple el quinto postulado de Euclides y por eso es un geometría NO euclidiana.

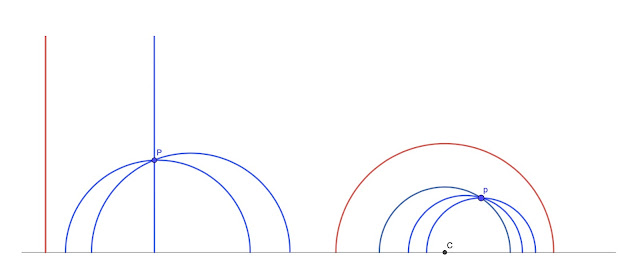
En el siguiente gráfico podemos ver dos rectas hiperbólicas (en color rojo), una vertical y otra semicircular, y varias rectas paralelas a ellas (en azul) por sendos puntos exterior (ambos denominados con la letra P):

Métrica hiperbólica

Definamos ahora la métrica de esta geometría es decir cómo medir la longitud de cualquier segmento. Empezaremos, como antes, con el caso de los segmentos verticales

En este caso, la longitud del segmento AB es log(b/a).

Definida así, la longitud del segmento AB es la misma que la del segmento A'B' transformado del AB por cualquier homotecia con centro en el eje horizontal:

En efecto, la longitud el segmento A'B' es log(kb/ka) que es igual que log(b/a).

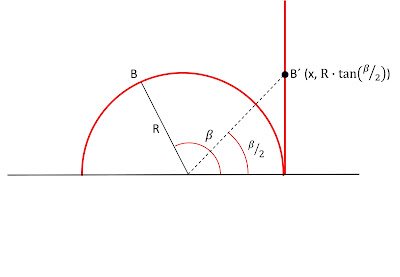
Definamos ahora la longitud de un segmento no vertical como el de la figura

Este segmento es equivalente en longitud a uno vertical que construiremos sobre una recta vertical tangente al semicírculo.

Empezamos con el punto A:

y seguimos con el punto B:

Ya tenemos el segmento vertical equivalente al AB:

La longitud del segmento AB la definimos como la del segmento A'B', es decir log[tan(β/2) / tan(α/2)], donde α y β son los ángulos correspondientes a los puntos A y B como hemos visto en las figuras anteriores.

Con esta métrica, en contraste con lo que sucede. con la métrica euclídea, la longitud de un segmento puede variar de forma sorprendente cuando el segmento se aleja hacia los extremos de la recta que lo contiene. Si A y B están en una recta vertical, digamos que con coordenadas (x0, y) y (x0, y+1) respectivamente, cuando el segmento AB se aleja hacia la parte superior de la recta, es decir cuando y tiende a infinito, la longitud del segmento tiende a 0; mientras que si el segmento se aleja hacia la parte inferior de la recta, es decir cuando y tiende a 0, entonces la longitud el segmento se hace cada vez más grande: tiende a infinito. En cambio, si A y B están en una recta semicircular, al acercarse a ambos extremos la longitud del segmento AB tiende a infinito.

Imaginemos dos hormigas recorriendo sendas rectas hiperbólicas verticales, siguiendo trayectorias paralelas, de forma que siempre se encontraran a la misma altura. Si fueran hacia la parte superior, la distancia entre ellas se iría reduciendo, tendiendo a 0; mientras que si se acercaran al eje horizontal, se irían alejando más y más entre ellas: su distancia tendería a infinito.

Algo parecido sucedería si, con la métrica euclidiana, cada hormiga recorriese una de las ramas de una hipérbola, por esa razón esta geometría se llamó hiperbólica.

El grupo de las isometrías en la geometría hiperbólica

Las transformaciones o movimientos que dejan invariantes las longitudes se llaman isometrías.

En el plano euclídeo sabemos que estos movimientos son las simetrías axiales, los giros y las traslaciones; y que todos ellos se pueden obtener componiendo, es decir aplicando sucesivamente, simetrías axiales. Así por ejemplo, si componemos dos simetrías axiales cuyos ejes se cortan, el resultado es un giro con centro en el punto de corte; mientras que si los ejes son paralelos, el resultado es una traslación en una dirección perpendicular a ambos ejes.

Por esta capacidad de componer isometrías para dar lugar a otras isometrías se dice que el conjunto de isometrías son un grupo, y nos referimos a ellas como el grupo de las isometrías.

Como dijimos al comienzo de esta entrada, las homotecias no son isometrías en el plano euclídeo pero sí lo son en el Semiplano de Poincaré.

El grupo de las isometrías hiperbólicas lo forman, junto a las homotecias, las traslaciones, las simetrías axiales y las inversiones, que son otro tipo de transformación en el plano que tampoco es una isometría euclidiana.

El eje de una simetrías axial hiperbólicas pueden ser cualquier recta hiperbólica, tanto las verticales como las semicirculares. En este último caso, el semidisco limitado por la recta semicircular se transforma en toda la porción de semiplano que queda por encima de ella y viceversa.

Geometría: un espacio y un grupo de transformaciones

Esta excursión por la geometría hiperbólica sólo pretende ilustrar la existencia de múltiples geometrías, en este caso la hiperbólica como una alternativa a la geometría clásica o euclidiana, señalando que los elementos  básicos, comunes a ellas dos y a todas las demás, son: un espacio (los puntos) y un grupo de transformaciones (las isometrías).

El dominio de cada geometría viene totalmente determinado por esos dos elementos pues todos los conceptos (rectas, métrica, ángulos, polígonos, etc.) que se manejan en cualquier geometría son aquellos que se mantienen invariantes por el grupo de transformaciones.